General Mathematics Paper 2,May/June. 2011

General Mathematics Paper 2, May/June. 2011

Questions:	1	2	3	4	5	6	7	8	9	10	11	12	13	Main

General Comments
Weakness/Remedies
Strength

Question 6
In a class of 40 students, 18 passed Mathematics, 19 passed Accounts, 16 passed Economics, 5 Mathematics and Accounts only,6 Mathematics only, 9 Accounts only,2 Accounts and Economics only. If each student offered at least one of the subjects, How many students failed in all the subjects? Find the percentage number who failed in at least one of Economics and Mathematics; Calculate the probability that a student selected at random failed in Accounts
_____________________________________________________________________________________________________
Observation
The Chief Examiner reported that this question was popular among the candidates and their performance was described as fair. Candidates were expected to represent the given information on a Venn diagram and label the diagram appropriately as shown M= 18 From the diagram, x (the number of those who passed all the subjects) = 19 – ( 5 + 9 + 2) = 3, where 19 is the number who passed in Accounts. Those who passed in Mathematics and Economics = 18 – (6 +5 + 3) = 4 while those who passed in Economics only = 16 – 4 – 3 – 2 = 7. Therefore, number who passed in at least one subject = n(M) + n(E) + 9 – x – 4 = 18 + 16 + 9 – 3 – 4 = 36. This implied that number who failed all the three subjects = 40 – 36 = 4. 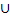Number who failed in at least one of Economics and Mathematics = 40 – n(ME) = 40 – 27 = 13. 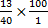Percentage who failed in at least one of Economics and Mathematics = = 32½ %. Number who failed in Accounts = 40 – n(A) = 40 – 19 = 21. 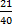Probability of selecting one who failed in Accounts = or 0.525. It was observed that majority of the candidates did not draw the Venn diagram correctly. This affected their correct interpretation and hence the solution of the question.