This question was very popular among the candidates.
Performance in part (a) was poor because many candidates ended up describing the simple pendulum experiment. Performance was average in part (b). In part (c) performance was poor because majority of the candidates failed to present acceptable/correct sketches. Hence they could not validly make the deductions sought.
The expected answers are as follows:
(a) PROCEDURE
Make at least 3 well-spaced pin holes round the edge of the cardboard. Clamp the pin horizontally and suspend the cardboard on it through one of the pin-holes such that the cardboard can swing freely
Hang the simple pendulum on the same pin and let its string be very close to the cardboard.
When the whole system is at rest (or in equilibrium) trace the plumbline on the cardboard. Repeat the procedure for each of the two other pin holes.
CONCLUSION
The point at which the (three) traced lines intersect is the centre of gravity of the cardboard.
PRECAUTIONS
- Repeat procedure
- Pin rigidly and firmly held by retort stand and clamp
- Allow the simple pendulum to rest before tracing the shadow of
the plumbline on the cardboard.
- The string to be close to the cardboard
11(b) Diagram:
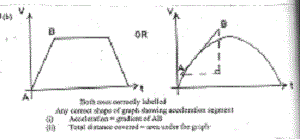
Both axes correctly labelled
Any correct shape of graph showing acceleration segment
- Acceleration = gradient of AB
- Total distance covered = area under the graph
11(c) Diagram
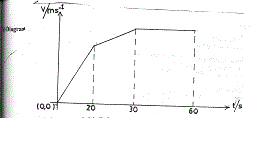
- At least one axis labelled
- correct shape of graph
Let V1 = maximum velocity after 20 sec.
V2 = maximum velocity after 30 sec.
(i) Then V1 = 6
20
∴ V1 = 120 ms-1
Also V2 – V1 = 4
10
V2 – V1 = 40
V2 = 120 + 40
V2 = 160 ms-1
Maximum speed = V2 = 160ms-1
(ii) Total distance covered = Area of Δ + Area of trapezium after 1st 30 seconds
= ( ½ x 20 x 120) + ½ (120 + 160) x 10
= 1200 + 1400
= 2600m
(iii) Average speed = Total distance
Total time
= 2600 30
= 86.67 ms-1



