|
|
Question 13
|
- A committee of five is to be formed among 6 Ghanaians, 8 Nigerians and 5 Gambians. In how many ways can the committee be formed if;
- there is no restriction;
- at most 2 Ghanaians are on the committee;
- 1 Nigerian is on the committee?
- Five out of 12 articles are known to be defective. If three articles are picked, one after the other without replacement, find the probability that all the three articles are non-defective.
|
| _____________________________________________________________________________________________________ |
|
This question was reportedly attempted by majority of the candidates. According to the
report, majority of the candidates who attempted the question performed better in part (a) than part (b). In part (a), candidates were expected to show that total number of persons
= 6 + 8 + 5 = 19. Five persons could be selected from 19 persons in 19C5 ways = 1168 ways. If two Ghanaians were on the committee, then number of ways of selection
= (6C0 x 13C5) + (6C1 x 13C4) + (6C2 x 13C3) = 9287 + 4290 + 4290 = 9867 ways. If 1 Nigerian was on the committee, then the number of ways of selection = 8C1 x 11C4 = 2640 ways.
In part (b), number of articles = 12, number of defective articles = 5. Therefore number of non-defective articles = 7. Prob(non-defective) = 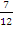 . Hence probability that all three are non-defective = . Hence probability that all three are non-defective = 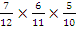 = = 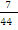 or 0.318182. or 0.318182. |
|
|
|



