The Chief Examiner reported that majority of the candidates attempted this question and their performance was described as fair. Majority of the candidates who attempted this question reportedly performed better in part (a) than in part (b).
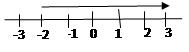
In part (a), the report stated that while majority of them were able to solve the inequality, a good number of them did not represent the solution on a number line correctly as required. Candidates were expected to remove the fraction by multiplying through by the L.C.M. which was 6 to obtain 3x – 5(x + 2) ≤ 6 + 6x. Expanding the left hand side and bringing like terms together gave x ≥ -2 and this was represented on a number line as
 

 

In part (b), it was observed that some candidates did not represent the given information in a diagram. Others did not draw the correct diagram. Majority of them reportedly applied wrong trigonometric ratios. Candidates were expected to illustrate the given information in a diagram as shown:
 

 

 

 

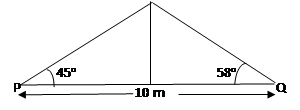
From the diagram, if h = height of pole and x m is the distance from P to the pole, then   = tan 45o or 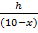 = tan 58o.
This implied that xtan 45o = (10 – x)tan 58o. Solving this equation gave x = 6.2 m. The height, h = xtan 45o = 6.2tan 45o = 6.2 m