Question 2
- Define the following quantities with respect to sinusoidal waveforms:
- average value;
- root mean square (r.m.s.) value;
- peak-to-peak value.
- The maximum value of a sinusoidal voltage is 230 V. Calculate its:
- root mean square (r.m.s.) value;
- Average value.
Observation
The expected responses were:
(a) (i)For the sinusoid, average value is defined as the average, taken over one half of the waveform’s period. It is given, in terms of its peak value, by. 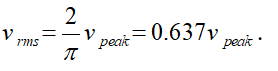
It is the reading of the ‘rectifier-type’ reading instrument.
(ii) A sinusoid’s rms (or effective) value is that value of dc current or voltage, which has these same heating effect as the ac voltage or current.
It is given by: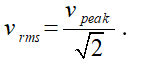 .
.
It is the reading of the ‘hot-wire’ type reading instrument
(iii) The peak-to-peak value of a sinusoid is the difference of its positive maximum and the magnitude of its negative maximum. It is twice the maximum or peak value.
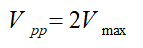

Question 2 required candidates to define certain properties (quantities) of sinusoidal waveforms in the first task and determine the values of same using given parameters in the second. According to the Chief Examiner, while majority of the candidates could define average value and only a few did for root mean square value in the first task, the reverse is the case in the second.
