The chief examiner reported that majority of the candidates attempted this question and many performed well.  However, some candidates could not interpret the relationship between a cone and an arc of a circle correctly.  While some candidates used the slant height of the cone as the height of the cone, others used the radius of the arc as the radius of the base of the cone.  A few other candidates were not able to draw the diagram correctly.
 

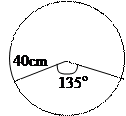
This diagram would have aided them to establish that the length of the arc of the circle = circumference of the base of the cone and that the radius of the sector = slant height of the cone. i.e. 135/360 x 2 x p x 40/1 = 2 x p x r where r = base radius of cone. Simplifying gave r = 15cm.

Slant height of cone, = l  =  40cm, r = 15cm. Using pythagoras theorem,
h2 + r2 = l 2  where h = perpendicular height of cone.
\ h = √402 – 152 = 37.081 cm.  Therefore volume of Cone = 1/3 x p x r2 x h

1 x 22 x 15 x 15 x 37.081   =  8741cm3 to the nearest cm3.
3     7          1             1