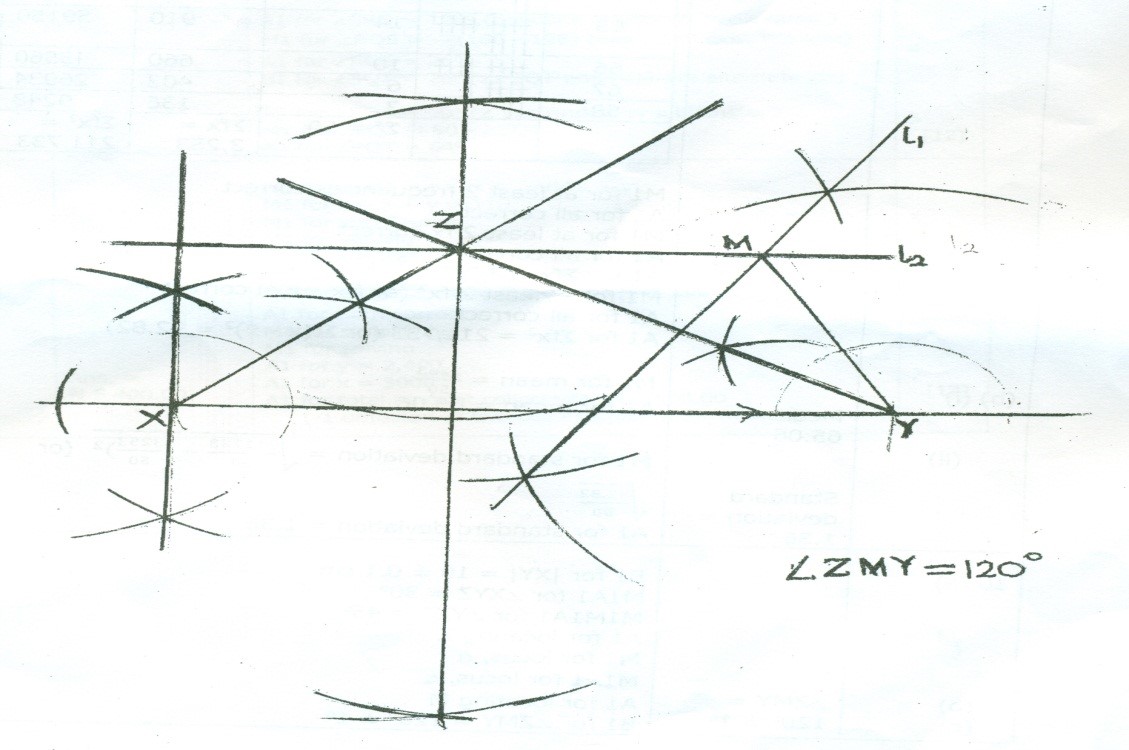
Question 10
Using ruler and a pair of compasses only,
- (a) construct:
(i) ∆XYZ such that │XY│ = 10 cm, ÐXYZ = 30o and ÐYXZ = 45o;
(ii) locus, ᶩ1, of points equidistant from Y and Z;
(iii) locus, ᶩ2, of points parallel to XY through Z.
- (b) Locate point M, the point of intersection of ᶩ1 and ᶩ2.
- (c)Measure ÐZMY.
Observation
This question was reported to be one of the least attractive question in the paper and very few of those who attempted it got the full marks. Teachers were encouraged to put more effort at making this topic more attractive to students.
Candidates were expected to draw the line XY to be 10cm long. At Y, candidates were expected to construct Ð60o and thereafter, bisect it to have Ð30o. Candidates were also expected to construct Ð90o at X and bisect it to have 45o. The point of intersection of the two bisectors was the point Z. Candidates were expected to join the three points to obtain the required triangle. The locus of points equidistant from Y and Z was the perpendicular bisector of the line joining points Y and Z. To obtain the locus of points parallel to XY through Z, candidates were expected to use the pair of compasses with centre at Z and the length, |XY| to draw an arc. Also, with centre at Y and the length │XZ│, draw another arc to cut the first arc. Join to point of intersection of the two arcs to the point Z and obtain the required locus. The point of intersection of the two loci was the required point M. Angle ZMY measured with a protractor gave 120o.