Question 3A
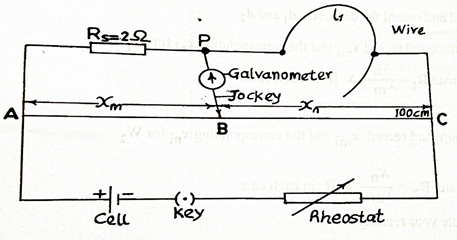
A standard resistor of resistance 2 Ω is connected in the left gap of the metre bridge and a length l1 of wire W1 is connected across the right gap of the bridge as shown in the diagram above. The balance point B is determined by touching the metre wire with the jockey. The balance length xm and xn are measured and recorded.
The procedure is repeated for five other values of length l.
The entire procedure is repeated using a second wire W2.
The diameters d1 of W1 and d2 of W2 are measured and recorded
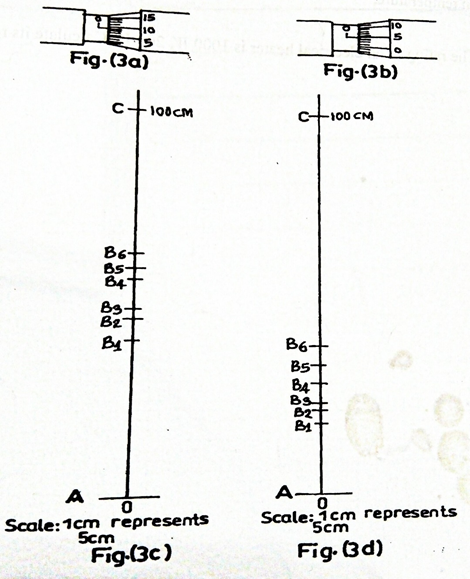
Fig. 3(a) and fig. 3(b) represent sections of a micrometer screw guage indicating the
readings of diameters d1 and d2 respectively.
Fig. 3(c) and fig. 3(d) show the positions Bi of the jockey on the metre wire for W1 and W2 respectively where i = 1, 2, 3, 4, 5 and 6.
- Read and record the diameter d1 and d2.
- Measure and record xmi and the corresponding xni for W1.
- Evaluate R1 = x R in each case.
- Measure and record xmi and the corresponding xni for W2.
- Tabulate your readings
- Plot a graph with R2 on the vertical axis and R1 on the horizontal axis.
- Determine the slope, s, of the graph.
- Determine the intercept, c, on the vertical axis.
- State two precautions that are necessary to ensure accurate results when performing this experiment.
(b) (i) Explain why the resistance of a metallic conductor increases with increase in temperature.
(ii) The rating of an electrical heater is 1000 W, 200V. Calculate its resistance.Observation
Part (a) This was popular question among the candidates. However, many candidates could not follow the given instructions in the question. measurement for w1 were mixed with w2. Also, some candidates invented their own values for xn and xm for the two wires.
Part (b) Candidates performance was poor. Most candidates could not explain why the resistance of a metallic conductor increases with increase in temperature.
The expected response is as stated below:
- Value of d1 correctly read and recorded to 2 d.p in mm
- Value of d2 correctly read and recorded to 2 d.p in mm
- Six values of Xm for W1 correctly measured and recorded
to at least 1 d.p and within tolerance of ± 0.1 cm
- Six values of Xm correctly converted
- Six values of Xn = (100 – Xm) correctly evaluated for W1
- Six values of R1 correctly evaluated to at least to 2 d.p
- Six values of Xm for W2 correctly measured and recorded to
at least 1 d.p and within tolerance of ± 0.1 cm
- Six values of Xm correctly converted
- Six values of Xn = (100 – Xm) correctly evaluated for W2
- Six values of R2 correctly evaluated to at least 2 d.p
- Plot a graph using reasonable scales
- draw line of best it
- determine the slope of the graph
- state any two of the following precautions.
e.g.
- Ensured tight terminals/tight connections
- Ensured clean terminals/clean terminals
- Avoid parallax error in reading metre rule/galvanometer
- Zero error noted/corrected on micrometer screw gauge/metre rule/galvanometer
- Open key when not taking readings
- Avoid sliding jockey on wire
- Repeated readings/repeat readings
b(i) A metal consist of free electrons in random motion. When the temperature of the metal is
increased, the vibration of the atoms is increased. This increases the number of collisions of the electrons with the atoms and therefore reduces the average velocity of electrons (conductivity). This results in the increase in the resistance of the metal.
OR
When the temperature of a metal is increased, the thermal vibrations of the atoms in the metal increases, this increases the interaction of the electrons with the crystal lattice, and therefore reduces the mobility of the electrons. The reduction in mobility of the electrons in the metal increases the resistance of the metal.
OR
The resistance (Ro) of a metal at temperature θ is related to the temperature by the equation: Rθ = Ro (1 + αθ) (where α is temperature coefficient of the resistance of the metal at 0oC). For metals α is positive, hence, resistance increases with increase in temperature.
OR
With increase in temperature of a metallic conductor, the length of the metal increases and since resistance is directly proportional to length, resistance increase.
