The report stated that this question was popular among the candidates and majority of them performed well in it. In part (a), majority of the candidates were reported to integrate the given gradient function 2x – 3x2 to obtain y = x2 – x3 + c and substitute (1, 2) into it to obtain c = 2. Hence the required equation was y = x2 – x3 + 2. Some candidates were reported to have differentiated the gradient function instead integrating it.
In part (b), candidates were expected to determine the points of intersection with the x-axis by substituting 0 for y in the equation y = x2 – 1 and factorizing to obtain x = -1 and 1. Hence the points were (-1, 0) and (1, 0). 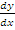 = 2x. At (-1, 0),
= 2x. At (-1, 0), 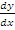 = -2 hence gradient of the normal at
= -2 hence gradient of the normal at
(-1, 0) = 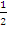 . Equation of the normal is y – 0 =
. Equation of the normal is y – 0 = 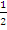 (x + 1) which reduced to x -2y + 1 = 0. Similarly, gradient at (1, 0) = 2.
(x + 1) which reduced to x -2y + 1 = 0. Similarly, gradient at (1, 0) = 2.
Hence gradient of normal = - 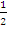 . Equation of normal is y – 0 = -
. Equation of normal is y – 0 = - 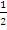 (x – 1) which simplified to x + 2y – 1 = 0. Solving x + 2y – 1 = 0 and x – 2y + 1 = 0 simultaneously would give the point of intersection which is (0,
(x – 1) which simplified to x + 2y – 1 = 0. Solving x + 2y – 1 = 0 and x – 2y + 1 = 0 simultaneously would give the point of intersection which is (0, 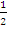 ).
).



