|
|
Question 16
|
- The position vectors of points P, Q and R are 5i + 3j, 8i – j and 11i – 5j respectively.
- Show that P, Q and R are collinear.
- Find the scalars k1 and k2 such that 37i – j = k1p + k2 r where p and r are position vectors of P and R respectively.
- Given that m = 3i – 4j and n = 6i + 4j, find the angle between the two vectors, correct to the nearest degree.
|
| _____________________________________________________________________________________________________ |
|
It was reported that this question was attempted by majority of the candidates and their performance was described as fair. Candidates were expected to respond as follows:
In part (a), gradient of PQ =  = = 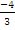 . Gradient of QR = . Gradient of QR = 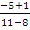 = = 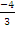 . Since the gradients were the same, it implied that the points were collinear. K1p + k2r = k1(5i + 3j) + k2(11i – 5j) = (5k1 + 11k2)i + (3k1 – 5k2)j. If k1p + k2r = 37i – j, then 5k1 + 11k2 = 37 and 3k1 – 5k2 = -1. Solving these equations simultaneously gave k1 = 3 and k2 = 2. . Since the gradients were the same, it implied that the points were collinear. K1p + k2r = k1(5i + 3j) + k2(11i – 5j) = (5k1 + 11k2)i + (3k1 – 5k2)j. If k1p + k2r = 37i – j, then 5k1 + 11k2 = 37 and 3k1 – 5k2 = -1. Solving these equations simultaneously gave k1 = 3 and k2 = 2.
In part (b), candidates were expected to recall that if θ was the angle between two vectors m and n, then cos θ = 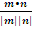 . Here, m = 3i – 4j and n = 6i + 4j. |m| = . Here, m = 3i – 4j and n = 6i + 4j. |m| = 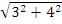 = 5. |n| = = 5. |n| = 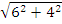 = = 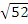 . Therefore, cos θ = . Therefore, cos θ = 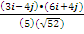 = = 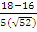 = 0.0555. hence, θ = cos-1(0.0555) = 86.82o = 87o to the nearest degree. = 0.0555. hence, θ = cos-1(0.0555) = 86.82o = 87o to the nearest degree.
. |
|
|
|



