|
Question 7 |
(a) A woman looking out from the window of a building at a height of 30m, observed that the angle of depression of the top of a flag pole was 44º. If the foot of the pole is 25m from the foot of the building and on the same horizontal ground, find, correct to the nearest whole number, the
(i) angle of depression of the foot of the pole from the woman;
(ii)height of the flag pole.
(b)
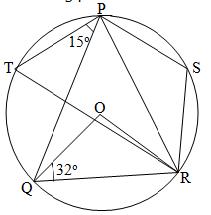
In the diagram, O is the centre of the circle, <OQR = 32º and <TPQ = 15º. Calculate:
(i) <QPR;
(ii) <TQO. |
| _____________________________________________________________________________________________________ |
|
|
This question was reported to be quite unpopular among the candidates, and candidates’ performance in it was said to be generally poor. Part (a) tested candidates’ knowledge of angle of elevation and depression. The main problem with majority of the candidates who attempted the question was on getting the diagram. They therefore scored very low marks. The correct diagram was as shown below:
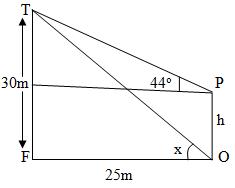
From the diagram, tan x = 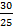 = 1.2. Hence x = tan -1(1.2) = 50°. = 1.2. Hence x = tan -1(1.2) = 50°.
Similarly, 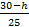 = tan 44°, therefore, h = 30 - 25tan 44° = 6m to the nearest metre. = tan 44°, therefore, h = 30 - 25tan 44° = 6m to the nearest metre.
In part (b), candidates were expected to apply some circle theorems to solve the problem. Many of them could not apply these theorems correctly. For instance <QOR = (180 – 2(32)) = 116° (sum of the angles of an isosceles triangle OQR).Hence <QPR = 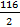 = 58° (angle at the centre is twice angle at the circumference) and <TQO = 180 – 32 - <QRP – 15° (opposite angles of a cyclic quadrilateralQTPR) = 75°. = 58° (angle at the centre is twice angle at the circumference) and <TQO = 180 – 32 - <QRP – 15° (opposite angles of a cyclic quadrilateralQTPR) = 75°. |
|
|



