|
Question 9 |
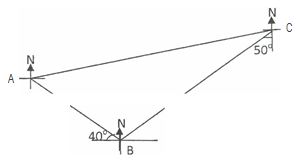
In the diagram, /AB/ = 8 km, /BC/ = 13 km, the bearing of A from B is 310° and the bearing of B
from C is 230°. Calculate, correct to 3 significant figures,
(a) the distance AC;
(b) the bearing of C from A;
(c) how far east of B, C is
|
| _____________________________________________________________________________________________________ |
|
This question was reported to have been attempted by majority of the candidates and their
performance was described as satisfactory. However, most of them were reported not to
calculate LABC correctly hence got wrong answers even though they were able to apply the
cosine rule correctly to their wrong values. Others were not able to determine the required
bearing correctly. The expected responses were as follows:
LASC = 100°. Therefore /AC/ = 82 + 132 - 2 (8)(13)cos100 which gave
/ AC/ = 16.4 km.
sin (LCAS) = sin100. Hence, sin (LCAB) = 13Sin100
13 16.4 16.4
Simplifying gave LCAB = 51.32°. Bearing of C from A = 180 - (50 + 51.32) = 079°.
If the distance of C east of B = BD, then BO = BC cas 40° = 13 x cas 40° = 9.96 km.
|
|
|
|



