Question 1A
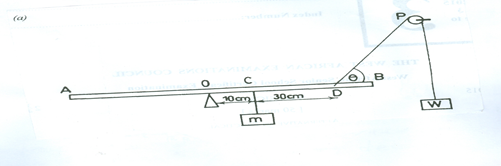
A uniform metre rule AB is pivoted at its mid-point O. A weight m is suspended at C a distance of 10cm from O. A string carry another weight W is attached to the metre rule at a point D, such that the distance CD = 30 cm. The string is passed through a pulley P such that it makes an angle with the metre rule when the rule balances horizontally.
The procedure is repeated for four other values of m ensuring in each case, that the pulley is adjusted until the rule balances again horizontally. The various weights m and the corresponding angles are measured and recorded.
Fig. 1(a) shows the values of the weights mi read on a spring while Fig. 1(b) shows the corresponding anglesθiwhich the string makes with the rule to balance it horizontally. wherei = 1, 2, 3, 4 and 5.

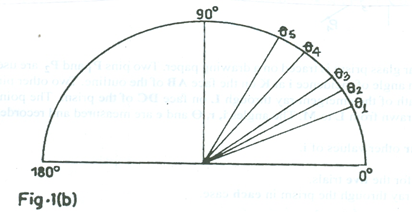
- Read and record the values of m using the given scale.
- Measure and record the corresponding values of
- Determine and record sin in each case.
- Tabulate your readings.
- Plot a graph with m on the vertical axis and sin on the horizontal
- Determine the slope, s, of the graph.
- From your graph, determine the value of m for which = 90o
- State two precautions that are necessary to ensure accurate results when
performing this experiment.
(b)(i)State the two laws governing the equilibrium of a body acted upon by parallel coplanar forces.
(ii) Write down the clockwise and anticlockwise moments about the pivot O in the diagram for the experiment.
Observation
Part (a) This was a popular question among the candidates. However, majority of the respondent candidates did not record the raw values of m but only the converted values. Even the converted values were not recorded to the required number of decimal places. Many candidates failed to determine correctly. The evaluation of sinwas not recorded to the required number of decimal places.
Few candidates that recorded m raw used it to plot the graph in disregardto the instruction. Many candidates did not extrapolate the graph to include sin = 1 hence, they could not determine the value of mfor which = 90o
Part (b). Majority of the candidates failed to write down the correct moment about pivot O in the diagram nor where they able to state the two laws governing the equilibrium of a body acted upon by parallel coplanar forces correctly because many of the candidates omitted the vital phrase “ about the same point or at a point” in their definition
Generally performance was average.
The expected answers are that candidates were expected to:
- Measure and record five values of mraw correctly to at least 1 d. p. in cm
and within tolerance of 0.1 cm
- Convert five values of m correctly to Newton/N
- Measure and record five values of correctly within tolerance of 1o
- Read and record five values of sin correctly to at least 3 d.p
- Show composite table of at least m, and Sin
- Distinguish graph axes correctly
- Chose reasonable scales
- Plot five points correctly
- Draw line of best fit.
- Evaluate slope of graph
- Deduce the value of m for which = 90, by evaluating sin 90o = 1. Trace the value
of 1 on graph and read off the corresponding value of m.
- State any two of the following precautions:
- Avoided parallax error in reading metre rule/protractor/spring balance
- Avoided draught
- Ensured the pulley was not stiff
- Ensured the weight was not resting/touching table
- Avoided zero error on the metre rule/spring balance
- Repeated readings stated
- Ensured firm/rigid support of the knife edge
Part (b)
(i) - The algebraic sum of the forces acting on the body is equal to zero. OR
- The sum of the forces in one direction is equal to the sum of the forces in the
opposite direction
- The sum of the clockwise moments at a point is equal to the sum of the
anticlockwise moments about the same point. OR
- The algebraic sum of the moments about a point is equal to zero.
(ii) Correct equation with terms correctly indicated
- Clockwise moment = (0.1 mg) Nm or (10 mg ) Ncm
- Anticlockwise moment = (0.4 W sin )Nm or (40 W sin )Ncm)
