Question 4
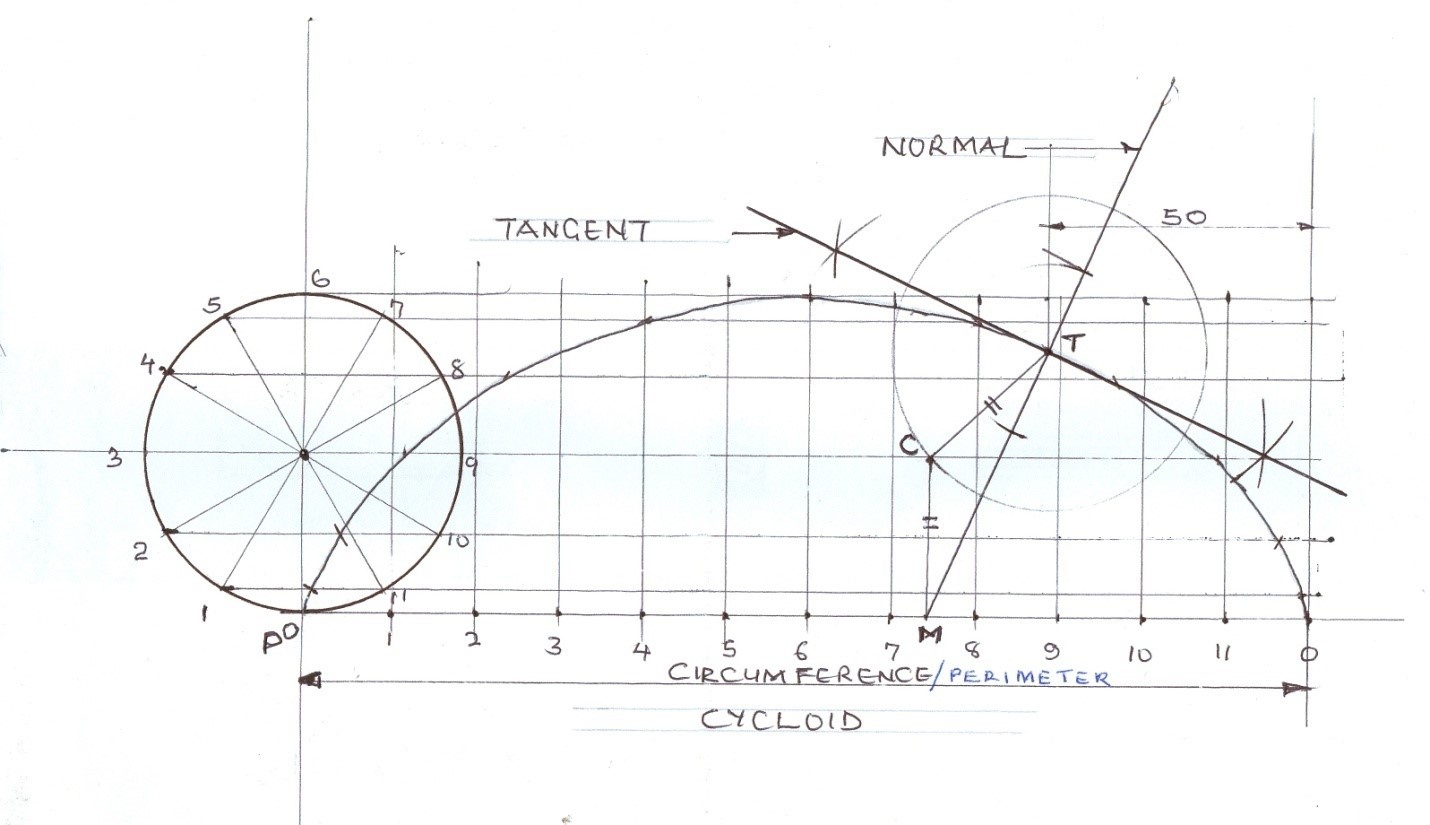
Plot the locus of a point P on the circumference of a circle diameter 60 rolling along a straight line without slipping.
Construct a tangent and a normal to the locus of a point 50 from the right end of the locus.
Observation
The candidates were required to draw a cycloid and then construct a tangent and a normal to the locus on a certain point on it.
Candidates were expected to do the following:
CYCLOID
A. DRAWING THE CYCLOID
(i) draw a straight line;
(ii) draw the circle Ø 60 tangential to the straight line and dividing it into 12 equal parts;
(iii) project lines from the divisional points on the circumference of the circle parallel to the straight lines;
(iv) transfer the divisional points on the circumference of the circle to locate the perimeter on the straight line;
(v) draw vertical lines on the divisional points on the perimeter;
(vi) locate the points for the cycloid;
(vii) join the points to obtain a smooth cycloid.
B. DRAWING THE TANGENT AND NORMAL
(i) locate the point of tangency T on the curve 50 from the right end of the curve;
(ii) use point T as centre to draw a circle Ø60 to intercept the centre line at point C;
(iii) draw a perpendicular from point C to the straight line to locate point M;
(iv) join point M to point T and extend for the normal;
(v) construct a perpendicular at T on line MT extended for the tangent.
The solution is shown below: