|
|
Question 15
|
- The probability that a patient recovers from a disease is 0.25. If 6 people are known to have contracted this disease, calculate the probability that:
- more than three people survived;
- at most 2 people survived.
- Two distinct numbers are selected at random from the set P = {2, 3, 4, 5, 6}. Find the probability that
- the sum of the two numbers is 8;
- one of the numbers is a factor of the other.
-
|
| _____________________________________________________________________________________________________ |
|
Candidates’ performance in this question was reported to be poor. The report further stated that majority of the candidates displayed poor knowledge of probability. Teachers were encouraged to emphasize this area of the syllabus while preparing candidates for the examination.
In part (a), candidates were expected to show that if the probability of recovering was 0.25, then the probability of not recovering = 1 – 0.25 = 0.75. They were also expected to know that the question followed a binomial distribution with n = 6, p = 0.25 and q = 0.75. Therefore, P(more than 3 people recovered) = 6C4 (0.25)4(0.75)2 + 6C5(0.25)5(0.75)1 + 6C6(0.25)6 = 0.0376, correct to 3 significant figures. Also, P(at most 2 people recovered) = 6C0(0.75)6 + 6C1(0.25)1(0.75)5 + 6C2(0.25)2(0.75)4 = 0.8306.
In part (b), candidates’ expected response was as follows:
Total number of selections = 5P2 = 20. Number of desired selection = {(2, 6), (6, 2), (3, 5),(5, 3)} = 4. Hence, probability =  = = 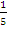 . The number of selections if one number is a factor of the other = {(2, 4), (4, 2), (2, 6),(6, 2), (3, 6), (6, 3)} = 6. Therefore, probability of selection where one number is a factor of the other was . The number of selections if one number is a factor of the other = {(2, 4), (4, 2), (2, 6),(6, 2), (3, 6), (6, 3)} = 6. Therefore, probability of selection where one number is a factor of the other was 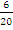 = = 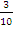 . . |
|
|
|



