|
Question 13 |
(a) P varies directly as Q and inversely as the square of R. If P = 1 when Q = 8 and R = 2, find the value of Q when P = 3 and R = 5.
(b) An aeroplane flies from town A(20oN, 60oE) to town B(20oN, 20oE).
(i) If the journey takes 6 hours, calculate, correct to 3 significant figures, the average speed of the aeroplane.
(ii) If it then flies due north from town B to town C, 420 km away, calculate, correct to the nearest degree, the latitude of town C.
[Take radius of the earth = 6400 km and π = 3.142] |
| _____________________________________________________________________________________________________ |
|
This question was reportedly attempted by majority of the candidates and their performance was commended. They showed significant strength on variation and their performance in longitude and latitude showed much improvement when compared with those of the previous years. Candidates were encouraged to take the issue of drawing diagrams seriously.
In part (a) the relationship between P, Q and R was P = 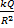 , where k was the constant of proportionality. Substituting the values of P, Q and R we obtained 1 = , where k was the constant of proportionality. Substituting the values of P, Q and R we obtained 1 = 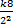 . Hence, k = . Hence, k =  . The relationship now became P = . The relationship now became P = 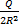 . When P = 3 and R = 5, Q = 2PR2 = 2(3)(5)2 = 150. . When P = 3 and R = 5, Q = 2PR2 = 2(3)(5)2 = 150.
In part (b), candidates were encouraged to draw the diagram as shown below.
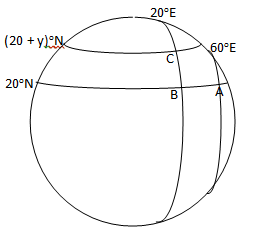
The first movement was along the parallel of latitude 20oN. Longitudinal difference = θ = 60o – 20o = 40o and radius of the earth, R = 6400km. Distance travelled = 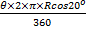 = = 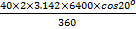 = 4199.13 km. Therefore average speed = = 4199.13 km. Therefore average speed = 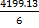 = 700 km/h correct to three significant figures. The second movement was along the parallel of longitude. If y was the change in latitude, then = 700 km/h correct to three significant figures. The second movement was along the parallel of longitude. If y was the change in latitude, then 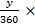 3.142 3.142  2 2  6400 = 420. Solving this gave y = 3.76o. Therefore Latitude of town C = 20o + 3.76o = 24oN approx. 6400 = 420. Solving this gave y = 3.76o. Therefore Latitude of town C = 20o + 3.76o = 24oN approx.
Questions 14 and 15 were not meant for candidates in Nigeria and responses were not received from them. |
|
|
|



