|
Question 3 |
A sector of a circle with radius 21 cm has an area of 280 cm2.
- Calculate, correct to 1 decimal place, the perimeter of the sector.
- If the sector is bent such that its straight edges coincide to form a cone, calculate, correct to the nearest degree, the vertical angle of the cone. [Take π =
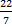 ] ]
|
| _____________________________________________________________________________________________________ |
|
This question was attempted by majority of the candidates and they performed very well in it. Majority of them were able to obtain the perimeter of the sector by comparing the formula for finding the area of a sector with that for finding the perimeter.
326
Since area of sector = 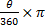 r2 = r2 = 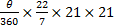 = 280, then = 280, then 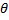 = = 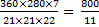 . .
Perimeter of sector = 2r + 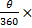 2πr = 2(21) + ( 2πr = 2(21) + ( 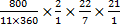 ) = 42 + ) = 42 + 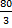 = 68.7 cm correct to one decimal place. = 68.7 cm correct to one decimal place.
When the sector is bent to form a cone, its radius becomes the slant height of the cone. The radius of the base of the cone is obtained from the relation r = 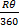 , where r = radius of the base of the cone, R = radius of the sector, θ = angle of the sector. Therefore r = , where r = radius of the base of the cone, R = radius of the sector, θ = angle of the sector. Therefore r = 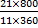 = = 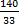 . If y is the vertical angle of the cone, then sin . If y is the vertical angle of the cone, then sin 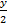 = =  = = 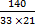 = 0.2020. Hence, required angle = y = 2 = 0.2020. Hence, required angle = y = 2  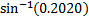 = 23o. = 23o. |
|
|
|



