|
Question 12 |
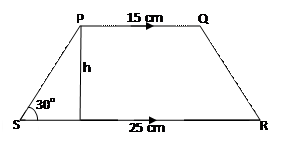
| (a)The area of trapezium PQRS is 60 cm2. PQ//RS, /PQ/ = 15 cm, /RS/ = 25 cm and
ÐPSR = 30o. Calculate the :
i)Perpendicular height of PQRS;
ii)|PS|.
(b)Ade received  of a sum of money, Nelly of a sum of money, Nelly  of the remainder while Austin took the rest. If Austin’s share is greater than Nelly’s share by N 3000, how much was did Ade receive? of the remainder while Austin took the rest. If Austin’s share is greater than Nelly’s share by N 3000, how much was did Ade receive? |
| _____________________________________________________________________________________________________ |
|
This question was attempted by majority of the candidates and they performed very well in it.
In part (a), one problem that was observed by the Chief Examiner was some candidates’ inability to draw the correct diagram. Candidates were encouraged to draw diagrams as this would help in solving problems in areas such as this. However, majority of the candidates were able to obtain the perpendicular height as well as the required angle as follows:
334
Area of trapezium = 60 = ½h(15 + 25), where h = perpendicular height. This implied that h = 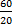 = 3 cm. h =|PS|sin30o. Hence, |PS| = = 3 cm. h =|PS|sin30o. Hence, |PS| = 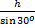 = = 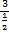 = 3 X 2 = 6cm. = 3 X 2 = 6cm.
In part (b), it was reported that candidates did not perform as well as they did in part (a). Many of them could not interpret the question correctly. Others were not able to manipulate the fractions well. Candidates were expected to respond as follows:
Let the amount of money be y, then Ade’s share =  y, Nelly’s share = y, Nelly’s share = 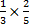 y = y = 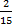 y. Therefore, Austin’s share = (1 – ( y. Therefore, Austin’s share = (1 – (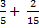 ))y = (1 - ))y = (1 - 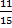 )y = )y = 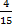 y. From the second statement, y. From the second statement, 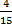 y - y - 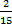 y = N 3,000, therefore, y = N 3,000, therefore, 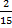 y = 3,000. This makes y = N 22,500.00. Hence, Ade’s share = y = 3,000. This makes y = N 22,500.00. Hence, Ade’s share = 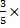 22500 = N 13,500 22500 = N 13,500 |
|
|
|



