Question 12
The table shows the distribution of marks of students in a Mathematics test.
|
3 |
4 |
5 |
6 |
7 |
8 |
9 |
Frequency |
1 |
4 |
3 |
5 |
2 |
|
2 |
If the mean of the distribution is 6, calculate the:
- value of
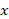 ;
; - standard deviation, correct to 2 decimal places.
Observation
The Chief Examiner reported that this question was the most popular question in section B. Majority of the candidates attempted it and they performed very well in it. The candidates were reported to apply the appropriate formula for calculating mean and standard deviation correctly. Candidates were reported to show that since 6 was the mean, then [(3 × 1) + (4 × 4) + (5 × 3) + (6 × 5) + (7 × 2) + (8 × x) + (9 × 2)] ÷[1 + 4 + 3 + 5 + 2 + x + 2] = 6. i.e. ![]() = 6.
= 6.
Solving this equation gave x = 3. Using the table
X |
f |
fx |
(x - |
f(x – |
3 |
1 |
3 |
-3 |
9 |
4 |
4 |
16 |
-2 |
16 |
5 |
3 |
15 |
-1 |
3 |
6 |
5 |
30 |
0 |
0 |
7 |
2 |
14 |
1 |
2 |
8 |
x(3) |
8x(24) |
2 |
12 |
9 |
2 |
18 |
3 |
18 |
|
Σf = (17 + x) = 20 |
Σfx = (96 + 8x) = 120 |
|
Σf(x – |
The standard deviation was calculated as ![]() =
= ![]() = 1.73, correct to 2 decimal places.
= 1.73, correct to 2 decimal places.
