The Chief Examiner reported that this was also an unpopular question as majority of the candidates did not attempt it. Candidates’ performance was also reported to be better in part (b) than in part (a).

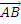
In part (a), candidates were expected to obtain, in vector components, the force acting along by multiplying the force by the unit vector in the direction of . 

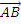
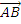
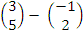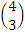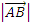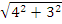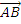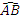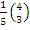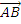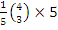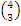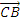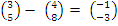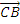= = .   =  = 5. Unit vector in the direction of   = = . Therefore, the force acting along  =  = N. Similarly, = .êê = 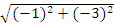 = 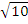. Unit vector in the direction of = .

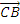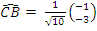Therefore the force acting along 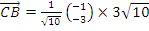 = 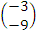N. The resultant force, R, was  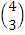+  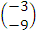= 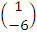N. The required direction was therefore obtained as  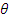=  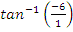= 171o or S9.47oE.

In part(b) candidates were reported to have performed well. They were reportedly able to apply the Newton’s laws of motion correctly. In part (i), candidates’ were expected to use the formula v2 = u2+ 2as where v = 20 ms-1, s = 8 m and u = 0 ms-1.

Substituting these values into the equation and solving gave a =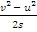 =  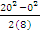=  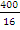= 25 ms-2. In part (ii), candidates were expected to apply the formula s = ut + 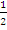at2. Here, s = 40 m, a = 25 ms-2 and u = 0 ms-1. Substituting these values into the formula and solving gave: 40 = 0(t) + 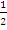(25)t2. i.e. 80 = 25t2. This implied that t =  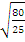= 1.8 seconds, correct to one decimal place.