QUESTION 7
(a)
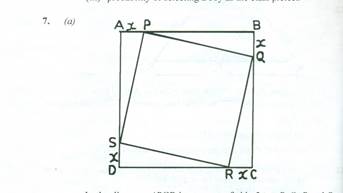
In the diagram, ABCD is a square of side 5 m. P, Q, R and S are points on
the square such that |AP| = |BQ| = |CR| = |DS| = x.
(i) Show that the area of the square PQRS is (2x2 – 10x + 25) m2.
(ii) Find, correct to two decimal places, the values of x for which the area of
PQRS is ![]() of that of ABCD.
of that of ABCD.
(b) If ![]() = d and 2s = n(a + l), express s in terms of n and d only.
= d and 2s = n(a + l), express s in terms of n and d only.
Observation
The Chief Examiner reported that the performance of majority of the candidates who attempted this question was also poor.
In part (a), candidates were expected to obtain the required equation by subtracting the sum of the areas of the triangles from that of the square ABCD. Since the triangles were congruent, their areas were equal. Area of a triangle = ![]() x(5 – x) =
x(5 – x) = ![]() (5x – x2). This implied that area of the 4 triangles = 2(5x – x2) = (10x – 2x2) m2. Area of ABCD = 52 = 25 m2. Therefore, area of PQRS = 25 – (10x – 2x2) = (2x2 – 10x + 25) m2. In part (a)(ii),
(5x – x2). This implied that area of the 4 triangles = 2(5x – x2) = (10x – 2x2) m2. Area of ABCD = 52 = 25 m2. Therefore, area of PQRS = 25 – (10x – 2x2) = (2x2 – 10x + 25) m2. In part (a)(ii), ![]() of 25 = 15. The values of x when the area of PQRS = 15 m2 was obtained by equating the expression for the area of PQRS to 15 and solving. i.e. 2x2 – 10x + 25 = 15 ≡ 2x2 – 10x + 10 = 0 ≡ x2 – 5x + 5 = 0. Solving this equation gave x = 1.38 m and 3.62 m.
of 25 = 15. The values of x when the area of PQRS = 15 m2 was obtained by equating the expression for the area of PQRS to 15 and solving. i.e. 2x2 – 10x + 25 = 15 ≡ 2x2 – 10x + 10 = 0 ≡ x2 – 5x + 5 = 0. Solving this equation gave x = 1.38 m and 3.62 m.
In part (b), cross multiplying the first equation gave (l + a) = d(n – 1). Substituting d(n – 1) for (l + a) in the second equation gave 2s = nd(n – 1). Hence, s = ![]() nd(n – 1).
nd(n – 1).
