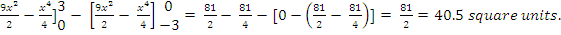This question was also reported to be quite popular among the candidates as majority of them attempted it. The report also stated that their performance was not as good as it was in question 10. However, their performance was reported to be better in part (a) than in part (b).
In part (a), candidates were expected to show that if f(x) =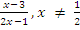 and g(x) = 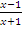, x ≠-1, gof = g() =   = =
.

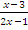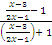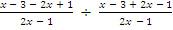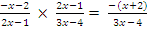In part (b), some candidates were reported to have plotted the graph instead of sketching it. Candidates were encouraged to read the question carefully and understand its demands before attempting them. In order to obtain a good sketch, candidates were expected to obtain the points of intersection of the curve and the axes as well as the turning points. The values of x at the points where the curve intersected the x-axis was obtained as follows:
On the x-axis, y = 0. That is 9x –x3 = 0. Factorizing this equation gave           x(3 + x)(3 - x) =0. This implied that the curve intersected the x-axis at the points where x = 0, -3 and 3. On the y-axis, x = 0. Hence, the point of intersection of the curve on the y-axis was obtained by substituting 0 for x in the equation to obtain y = 9(0) – (0)3 = 0. Therefore the curve passes through points (-3, 0), (0, 0) and (3. 0). To find the turning points, candidates’ were expected to differentiate y with respect to x to obtain 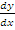 = 9 – 3x2. At the turning points,  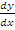= 0 i.e. 9 – 3x2= 0. Solving this equation gave x = 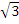and - . 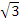The values of y at these points were obtained by substituting  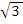and -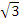 respectively for x as follows:

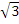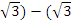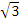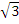When x = ,y = 9()3 = 9  – 3= 6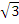. When x = -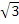,  y = 9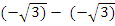3 = -9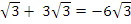.The required sketch was

 

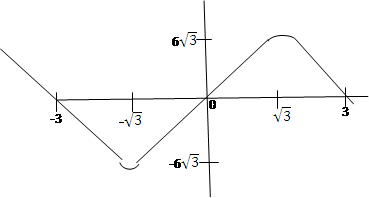
The total area bounded by the curve and the x-axis was obtained as
Total area =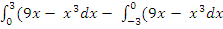 = [