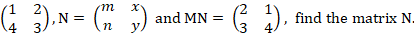
Observation

The Chief Examiner reported that this question was popular among the Candidates’. They showed mastery of the concept of completing the Squares. However, the conceptual issue of approximation was still obvious. It was then pointed out in the report that this should be taught rigorously by Mathematics Teachers.
In part (a), the Candidates’ solved as expected by dividing through by 3 to get y2  y = , then adding the square of half the coefficient of y to both sides and simplifying to get , therefore, y = 1.00 or y = 0.67 (2 decimal places).
In part (b), the Candidates’ performed the operation of multiplication of matrices correctly, they showed that:
MN =
Next they equated and compared terms to get the set of simultaneous equations:
m + 2n = 2…………………………………………………(1)
x + 2y = 1………………………………………………….(2)
4m + 3n = 3 ……………………………………………….(3)
4x + 3y = 4 …………………………………………………(4)
Solving the equations (1) and (3) simultaneously and equations (2) and (4) simultaneously to get m = 0, n = 1, x = 1and y = 0.
Then, the matrix N = .