Question 2
- Solve the equation:
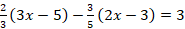 .
.
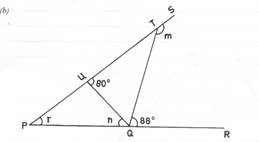
In the diagram, < STQ = m, < TUQ = 800, < UPQ = r, < PQU = n and < RQT = 880. Find the value of (m + n).
Observation
In part (a), the Chief Examiner reported that the Candidates’ performance was quite high and encouraging as they got this right. They were required to multiply through by 15, which is the L.C.M. and this will yield 10(3x – 5) – 9(2x – 3) = 45. After which they expanded to obtain 30x – 50 – 18x + 27 = 45 and solving the equation to get x = ![]() or 5.67.
or 5.67.
In part (b), this question involves the application of some geometrical theorems such as “sum of angles on a straight line which is 1800; sum of angles in a triangle which is 1800 and the exterior angle in a triangle is equal to the sum of two interior angles. The Chief Examiner reported that most of the Candidates’ could not relate the given angles to the required (m + n), thereby applying the theorems wrongly. Candidates were expected to write n + r = 800 and 1800 – (m + r) = 880 and then solve to obtain m + n = 1720.
