Question 8
Marks |
1 |
2 |
3 |
4 |
5 |
Number of students |
m + 2 |
m – 1 |
2m – 3 |
m + 5 |
3m – 4 |
The table shows the distribution of marks scored by some students in a test.
- If the mean mark is
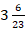, find the value of m. - Find the:
(i) inter-quartile range;
(ii) probability of selecting a student who scored at least 4 marks in the test.
Observation
The Chief Examiner reported that majority of the Candidates’ answered this question correctly but few had problems with the notation at least as they assumed it to be at most.
In part (a), the candidates’ did as expected by completing the fx column and summing as appropriate. They were expected to obtain the following table:
x |
1 |
2 |
3 |
4 |
5 |
Total |
f |
m+2 |
m-1 |
2m-3 |
m+5 |
3m-4 |
8m-1 |
fx |
m+2 |
2m-2 |
6m-9 |
4m+20 |
15m-20 |
28m-9 |
From the table, 
and 
, so that 
and solving yields m = 3.
In part (b) (i), since m has been gotten to be 3, the table then becomes:
x |
1 |
2 |
3 |
4 |
5 |
f |
5 |
2 |
3 |
8 |
5 |
Cf |
5 |
7 |
10 |
18 |
23 |
Therefore, interquartile range = 4 – 2 = 2.
Finally, in part (b) (ii), the probability of selecting a student who scored at least 4 marks is 
whereas most Candidates’ made use of at most 4 marks to obtain 
. Mathematics teachers are therefore advised to drill the students on the concept of probability as well as how do distinguish between “at least” and “at most”.