n part (a), it was reported that although this question was attempted by majority of the candidates, only those candidates who sketched the diagram correctly performed well on the question.
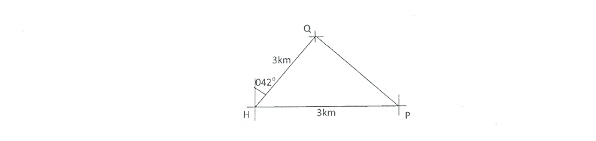The distance between the two ships could be obtained using either the sine or the cosine rule.
From the diagram, ∠QHP = 900 - 420 = 480. This implies that ∠HQP = LQPH = 180;48 = 660. Using
                                                                                                                                            2
the sine rule, sin66° = Sjin480•Therefore, /PQ/ = 3~in4~O = 2.44km. Recall that LQPH = 66°.
                           3               PQI                                       sin66°
Therefore, Bearing of Q from P = 270° + 66° = 336°.
In part (b), candidates' performance was reported to be poor. Candidates performed better in part (a) than in part (b). They were expected to relate the time-taken during each part of the journey with the total time for the whole journey. According to the report, their apparent difficulty was in recalling the fact that average speed = total distance . Candidates wereexpecte to lnd t e time taken for t e whole Journey as    
                 total time taken
           total distance covered  =  600  =10hrs.
                     average speed           60
lime taken when travelling with 75 krn/h = 300 = 4hrs. Therefore, time taken when travelling
                                                                             75
with v km/h = (10 - 4) hrs = 6hrs. i.e. 300= 6. Hence, v = 300 = 50km/h.
                                                                   v                              6