The Chief Examiner reported that this question was attempted by majority of the candidates. The report further stated that candidates’ performance in part (b) was better than what it was in part (a).
In part (a), it was reported that majority of the candidates did not recognize that the expression was that of difference of two squares and as a result, were not able to factorize the expression as required. Candidates were expected to factorize m2 – 2mn + n2 to obtain (m – n)2. This therefore meant that the expression m2 – 2mn + n2 – 9r2 was equivalent to (m – n)2 – 9r2 which by method of difference of two squares factorized further as
((m – n) + 3r)((m – n) – 3r) i.e. (m – n + 3r)(m – n – 3r).
In part (b), it was reported that some candidates could not obtain the second equation. They were expected to express both sides of the equality in index form with the same base and equate the indices. 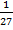expressed in index form was 3-3. The second equation would now be 33(y – x) = 3-3 which implied that 3(y – x) = -3 or y – x = -1. Solving this equation with the first one simultaneously gave x = 2 and y = 1.