|
Question 13
|
-
If x = 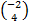 and y= 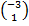 , find, correct to 1 decimal place, | x + y|.
-
P(6, 4), Q(-2, -2) and R(4, -6) are the vertices of triangle PQR.
-
Determine the coordinates of M and S, the midpoints of 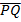 and 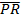 respectively.
-
Find 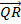 and 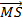 .
-
State the relationship between 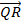 and 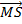 .
-
Find the equation of 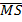 .
|
|
The Chief Examiner reported that this question was the most unpopular question and majority of those who attempted it performed poorly.
In part (a), candidates were expected respond as follows:
x + y = 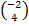 + + 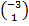 = =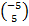 . Therefore, |x + y| = . Therefore, |x + y| = 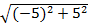 = 5 = 5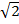 = 7.1. = 7.1.
In part (b), candidates were expected to show that if M(x, y) was the midpoint of 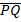 , then x = , then x = 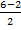 = 2 and y = = 2 and y = 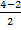 = 1. Hence, the required point was M(2, 1). Similarly, if S(x, y) was the midpoint of = 1. Hence, the required point was M(2, 1). Similarly, if S(x, y) was the midpoint of 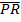 , then, x = , then, x = 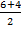 = 5 and y = = 5 and y = 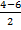 = -1. Therefore, the midpoint of = -1. Therefore, the midpoint of 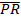 was S(5, -1). was S(5, -1). 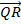 = = 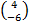 - - 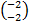 = = 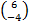 . Similarly, . Similarly, 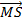 = = 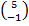 - - 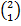 = = 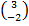 . By comparing the two vectors they would conclude that . By comparing the two vectors they would conclude that 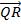 = 2 = 2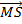 . To find the equation of . To find the equation of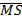 , candidates would first find the gradient of , candidates would first find the gradient of 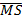 as as 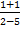 = = 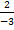 . The required equation was y – 1 = . The required equation was y – 1 =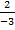 (x – 2) which simplified to 2x + 3y = 7. (x – 2) which simplified to 2x + 3y = 7.
|
|
|
|



