|
|
Question 10
|
- An exponential sequence is given by 18, 2, 2/9, …
Find (i) an expression for the nth term;
(ii) the sum of the first n terms.
(b)(i) Find the equation of the tangent to the curve y = -x2 + x + 1 at point (2, -1).
(ii) Find the intercepts of the tangent in (b)(i) with the axes.
|
| _____________________________________________________________________________________________________ |
|
This question was reported to be very popular among the candidates and they performed very well in it. They were able to derive the nth term of the sequence thus: a = 18, r = 1/9, nth term = arn - 1 = 18(1/9)n – 1 = 162(1/9)n.
The sum is derived thus: Sn = 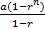 = =  = = 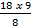 (1 – ( (1 – (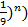 = = 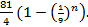
In part (b) candidates were expected to differentiate y = -x2 + x + 1 to obtain 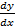 = -2x + 1 at (2, -1), = -2x + 1 at (2, -1), 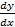 = -4 + 1 = -3. The equation of the tangent is gotten by y + 1 = -3(x – 2) º y + 3x – 5 = 0. On the x – axis, y = 0 ⇒ 3x = 5 or x = 5/3. Thus the tangent intercepts the x – axis at (5/3, 0). Similarly on the y-axis, x = 0. Thus y = 5. Hence the point of intersection = (0,5). = -4 + 1 = -3. The equation of the tangent is gotten by y + 1 = -3(x – 2) º y + 3x – 5 = 0. On the x – axis, y = 0 ⇒ 3x = 5 or x = 5/3. Thus the tangent intercepts the x – axis at (5/3, 0). Similarly on the y-axis, x = 0. Thus y = 5. Hence the point of intersection = (0,5). |
|
|
|



