|
|
Question 16
|
- Find the unit vector along the resultant of vectors (3i – 2j) and (i + 3j).
- The position vectors of points P, Q, R and S are
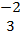 , , 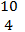 , , 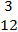 , , 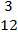 and and 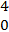 respectively. respectively.
- show that
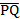 is perpendicular to is perpendicular to 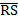
- calculate , correct to one decimal place, angle PSQ
|
| _____________________________________________________________________________________________________ |
|
The report stated that candidates found this question rather challenging. Although, they performed better in part (a) than in (b), their performance was generally poor. Teachers need to put in more effort during instruction. Candidates were expected to obtain the resultant of (3i – 2j) and (i + 5j) as
R = (3i – 2j) + (i + 5j) = 4i + 3j. /R/ = 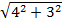 = 5. Therefore the unit vector in the direction of R = 1/5(4i + 3j) = 4/5i + 3/5j. = 5. Therefore the unit vector in the direction of R = 1/5(4i + 3j) = 4/5i + 3/5j.
In part (b), 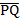 = = 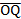 - - 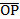 = =  - - 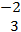 = = 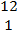 . .  = =  – – 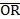 = = 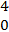 - - 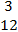
= 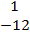 . . 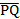 · · 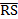 = = 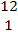 · ·  = 12 – 12 = 0 which implied that they were = 12 – 12 = 0 which implied that they were
perpendicular. 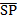 = = 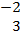 - - 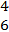 = = 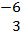 . . 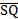 = = 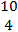 - - 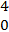 = = 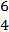
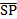 · · 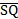 = = 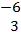 · · 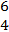 = -36 + 12 = -24. / = -36 + 12 = -24. /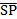 / = (-6)2 + 32 = 6.708 or / = (-6)2 + 32 = 6.708 or 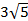
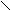 / /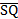 / = 62 + 42 = 7.211 or 2 / = 62 + 42 = 7.211 or 2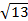 . Hence, cos < PSQ = . Hence, cos < PSQ = 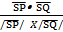 = = 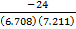 or or 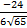 = -0.4962. Thus <PSQ = 119.8o to 1 decimal place. = -0.4962. Thus <PSQ = 119.8o to 1 decimal place. |
|
|
|



