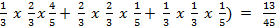Only very few candidates reportedly performed well in this question. Majority of them displayed poor knowledge of the probability of independent events. They were expected to show that if P(H1) = 1/3, P(H2) = 2/3 and P(H3) = 1/5 are the probabilities of each hunter hitting the target, then the probability of none of them hitting the target = P(H’1) x P(H’2) x P(H’3) = 2/3 x 1/3 x 4/5 = 8/45, where p(H1’), p(H2’) and p(H3’) are the probabilities of each hunter not hitting the target respectively. Therefore probability of at least one of them hit = 1 – prob. that none of them hit = 1 – 8/45 = 37/45.
Probability of only two of them hitting the target = P(H1 H2 H’3 + H’1 H2 H3 + H1 H’2 H3) = (