(a) If a student is selected at random from the group, find the probability that this student scored at most 69 marks.
(b) Calculate the median of the distribution.
It was reported that this question was well attempted by most candidates. They were able to determine the number of students who scored at most 69 as 73. Total number of students = 80. Therefore required probability = 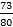 .
.
In part (b), candidates were expected to apply the formula,
Median = L1 + (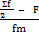 )c where L1 = lower class boundary of the median class = 39.5, Sf = total number of students = 80, F = cumulative frequency before the median class = 31, fm = frequency of the median class = 18 and c = median class width i.e. 39.5 + (
)c where L1 = lower class boundary of the median class = 39.5, Sf = total number of students = 80, F = cumulative frequency before the median class = 31, fm = frequency of the median class = 18 and c = median class width i.e. 39.5 + (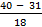 )10 = 44.5.
)10 = 44.5.



