The Chief Examiner reported that majority of the candidates did not attempt this question on permutation. The few who attempted it displayed poor knowledge of the topic. The expected response was thus:
nP3 = 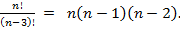 n-2P2 = n-2P2 = 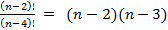 . .
This implied that n(n – 1)(n – 2) = 10(n – 2)(n – 3) i.e. n2 – 11n + 30 = 0 where on solving this equation gave n = 6 or 5.
Candidates’ performance in part (b) was reportedly better than in part (a). The few who solved the problem correctly were able to recognize it as a problem on combination and were able to obtain the number of choosing 4 persons as 10C4 = 210 ways.
In part (ii), choosing equal number of boys and girls implied choosing 2 boys and 2 girls. Number of ways of choosing 2 boys = 4C2 = 6. Number of ways of choosing 2 girls = 6C2 = 15. Therefore, number of ways of choosing equal number of boys and girls = 6 x 15 = 90. Probability of equal number = 90/210 = 3/7. |



