QUESTION 10
(a).
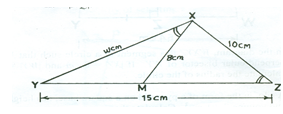
In the diagram, ∠YXM = ∠XZM, YZ is a straight line, |XM| = 8 cm,
|XZ| = 10 cm, |YZ| = 15 cm and |XY| = w cm. Find the value of w.
(b) A ship leaves port P and sails on a bearing of N 45 oE to a port Q, 15 km
away. It then sails on a bearing of S 45 o E to port R, 20 km away.
(i) Represent the information in a diagram
(ii) Calculate, correct to the nearest whole number, the:
I. distance from P to R;
II. bearing of P from R.
Observation
The Chief Examiner reported that majority of the candidates attempted this question and their performance was described as fair. Majority of the candidates who attempted this question reportedly performed better in part (b) than in part (a).
In part (a), the report stated that majority of the candidate did not correctly identify the triangles that were similar. Candidates were expected to recognize that triangles XYM and YZX were similar hence, 
= 
. Solving this equation gave w = 12 cm.
In part (b), it was observed that majority of the candidates were able to represent the given information in a diagram. Majority of them were also reported to calculate the distance from P to R but did not calculate the bearing of P from R correctly. Candidates were expected to illustrate the given information in a diagram as shown:
From the diagram, angle PQR = 90o. This implied that triangle PQR is a right angled triangle with PR as its hypotenuse. Using Pythagoras theorem, the distance from P to R = |PR| = 
= 
= 25 km, correct to the nearest whole number. The bearing of P from R was gotten as follows:
∠PRQ = tan-1(
) = 36.87o. ∠QRN = 45o (alternate angle to the bearing of R from Q). Therefore, required bearing = N (45 + 36.87)o W = N 82oW or 278o, correct to the nearest whole number.