QUESTION 11
The table shows the marks distribution of candidates selected for an award.
Marks (%) |
56 - 58 |
59 - 61 |
62 - 64 |
65 - 67 |
68 - 70 |
71 - 73 |
74 - 76 |
77 - 79 |
80 - 82 |
83 - 85 |
Frequency |
10 |
28 |
40 |
92 |
140 |
90 |
50 |
30 |
15 |
5 |
(a). Construct a cumulative frequency distribution table.
(b). Draw a cumulative frequency curve for the distribution.
(c). Use the curve to estimate the:
(i) Median mark;
(ii) Probability of selecting a candidate who scored not more than 72%.
Observation
This question was reported to be attempted by majority of the candidates and while they performed very well in parts (a) and (b), they performed poorly in part (c). In part (a), majority of the candidates were reported to correctly constructed the cumulative frequency table as shown below:
Marks (%) |
Lower Boundary |
Upper Boundary |
Frequency (f) |
Cumulative frequency |
56 – 58 |
55.5 |
58.5 |
10 |
10 |
59 – 61 |
58.5 |
61.5 |
28 |
38 |
62 – 64 |
61.5 |
64.5 |
40 |
78 |
65 – 67 |
64.5 |
67.5 |
92 |
170 |
68 – 70 |
67.5 |
70.5 |
140 |
310 |
71 – 73 |
70.5 |
73.5 |
90 |
400 |
74 – 76 |
73.5 |
76.5 |
50 |
450 |
77 – 79 |
76.5 |
79.5 |
30 |
480 |
80 – 82 |
79.5 |
82.5 |
15 |
495 |
83 – 85 |
82.5 |
85.5 |
5 |
500 |
Majority of them were also reported to draw the cumulative frequency curve.
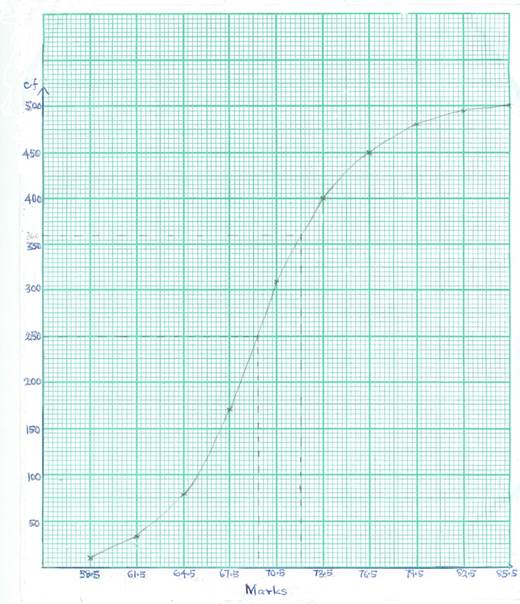
In part (c), candidates should know that the median mark was the mark corresponding to half the cumulative frequency. Half of 500 is 250. The mark corresponding to 250 as shown in the graph = 69.3% (± 0.3). To find the probability of selecting a candidate who scored not more than 72%, candidates should estimate from the graph, the number of students who scored not more than 72%. This should be done by locating 72 on the marks axis, trace it to the curve and read off the corresponding value on the cumulative frequency axis. This value was 355 (± 5). Therefore, required probability = ![]() = 0.71 (± 0.01).
= 0.71 (± 0.01).
