QUESTION 12
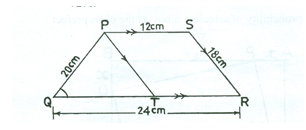
In the diagram, PS||QR, PT||SR, |QR| = 24 cm, |SR| = 18 cm, |PQ| = 20 cm and |PS| = 12 cm. Calculate, correct to 3 significant figures:
(a). ∠PQT;
(b). the height of triangle PQT
(c). the area of PTRS as a percentage of the area of PQRS.
Observation
The Chief Examiner reported that this question was quite unpopular among the candidates and the performance of those who attempted it was reported to be better in parts (a) and (b) but poor in part (c).
In part (a), candidates’ expected response was as follows:
|SR| = |PT| = 18 cm and |PS| = |TR| = 12 cm (opposite sides of parallelogram PTRS). This implied that |QT| = 24 - |TR| = 24 – 12 = 12 cm. Taking triangle QPT, by the cosine rule, cos(∠PQT) = ![]() = 0.4583. Therefore, ∠PQT = cos-1(0.4583) = 62.7o, correct to 3 significant figures. Height of triangle PQT = 20sin 62.7o = 17.8 cm, correct to 3 significant figures. In part (c), candidates should know that height of triangle PQT = height of parallelogram, PTRS = height of trapezium, PQRS = 17.8 cm. Therefore, Area of PTRS = base × height = 12 × 17.772 = 213.268 cm2. Area of PQRS =
= 0.4583. Therefore, ∠PQT = cos-1(0.4583) = 62.7o, correct to 3 significant figures. Height of triangle PQT = 20sin 62.7o = 17.8 cm, correct to 3 significant figures. In part (c), candidates should know that height of triangle PQT = height of parallelogram, PTRS = height of trapezium, PQRS = 17.8 cm. Therefore, Area of PTRS = base × height = 12 × 17.772 = 213.268 cm2. Area of PQRS = ![]() (sum of parallel sides) × height =
(sum of parallel sides) × height = ![]() (24 + 12) × 17.772 = 319.896 cm2. Therefore, required percentage =
(24 + 12) × 17.772 = 319.896 cm2. Therefore, required percentage = ![]() = 66.7%.
= 66.7%.
