QUESTION 8
(a)
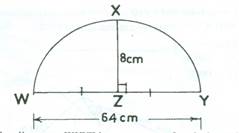
In the diagram, WXYZ is a segment of a circle such that XZ is the
perpendicular bisector of WY. If |XZ| = 8 cm and |WY| = 64 cm, calculate
the radius of the circle.
-
(a). A silo in the form of a pyramid on a square base, has height 27 cm and
volume 2601 cm3. Calculate the:
(i). length of a side of the base of the silo, correct to 3 significant figures;
(ii). angle between a sloping face and the base of the silo, correct to the nearest degree.
Observation
The Chief Examiner reported that this was another question where majority of the candidates performed poorly. According to the report, majority of those who attempted it did not illustrate the given information in a diagram.
In part (a), candidates were expected to recall the theorem which states that a perpendicular bisector of a chord passes through the centre of the circle. This implied that the line XZ if produced would pass through the centre of the circle as illustrated below:
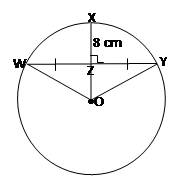
Let O be the centre of the circle and r be the radius. Then, |OW| = |OX| = r. By
pythagoras theorem, |OW|2 = |OZ|2 + |WZ|2. i.e. r2 = (r – 8)2 + 322. Solving this
equation gave r = 68.0 cm, correct to 3 significant figures.
in part (b), candidates were expected to draw the following diagram (or equivalent):
Candidates should recall that volume of pyramid = ![]() × area of base × height. Here, since the base is a square of side y, then the area of the base = y2, volume = 2601 cm3 and height = 27 cm. i.e. 2601 =
× area of base × height. Here, since the base is a square of side y, then the area of the base = y2, volume = 2601 cm3 and height = 27 cm. i.e. 2601 = ![]() 27y2. Solving this equation gave y = 17 cm. Candidates should know that angle between a sloping face (such as UPS) and the base of the pyramid (PQRS) = x (as shown in the diagram). To find the value of x, candidates should apply appropriate trigonometric ratios to triangle OUT. Here, |TO| =
27y2. Solving this equation gave y = 17 cm. Candidates should know that angle between a sloping face (such as UPS) and the base of the pyramid (PQRS) = x (as shown in the diagram). To find the value of x, candidates should apply appropriate trigonometric ratios to triangle OUT. Here, |TO| = ![]() × |SR| =
× |SR| = ![]() × 17 = 8.5 cm, |OU| = h = 27 cm. Using tan x =
× 17 = 8.5 cm, |OU| = h = 27 cm. Using tan x = ![]() , x = tan-1(
, x = tan-1(![]() ) = 73o, correct to the nearest degree.
) = 73o, correct to the nearest degree.
