QUESTION 9
(a). 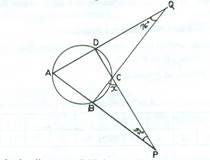
In the diagram, ABCD is a cyclic quadrilateral. AB and DC are produced to meet at P, AD and BC are produced to meet at Q. If ∠DQC = 76o, ∠BPC = 52o
and ∠BCP = x, calculate the value of x.
-
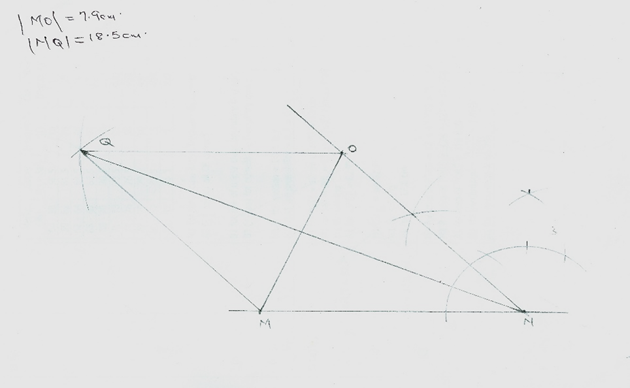
(b). (i). Using ruler and a pair of compasses only, construct a rhombus MNOQ
of length 10 cm and ∠MNO = 45o.
(ii) Measure:
I. |MO|;
II. |NQ|
Observation
The Chief Examiner reported that this question was quite unpopular among the candidates. Majority of them were reported not to attempt this question. Candidates as well as teachers were encouraged to put in more effort in the teaching and learning of geometry. In part (a), candidates were expected to recognize that ∠DCQ = ∠BCP = x (vertically opposite angles). This implied that ∠ADC = (76o + x) (exterior angle of triangle DQC). Similarly, ∠ABC = (52o + x) (exterior angle of triangle BPC). Since ABCD was a cyclic quadrilateral, it implied that (76o + x) + (52o + x) = 180o (opposite angles of a cyclic quadrilateral). Solving this equation gave x = 26o.
In part (b), candidates were expected to recall the properties of a rhombus such as opposite sides are parallel and all sides are equal. In constructing the rhombus, candidates were to draw a straight line and mark a point M on the line. Thereafter, they would locate point N by marking the point on the line which was 10 cm from M. At point N, they would construct angle 45o. They would then locate point O such that |ON| = 10 cm. At point M and using a length of 10 cm, candidates would draw an arc. At point O and using the same length, they would draw an arc to intersect the first arc. The point of intersection of the two arcs was the point Q. They would then join the points M, N, O and Q to obtain the required rhombus. With the ruler, candidates were expected to measure the lengths MO and NQ. |MO| = 7.8 cm while |NQ| = 18.5 cm (± 0.1 cm)