QUESTION 13
-
(a). Using a scale of 2 cm to 2 units on both axes, draw on a graph sheet, two
perpendicular axes 0x and 0y for -10 ≤ x ≤ 10 and -10 ≤ y ≤ 10.
(b). Draw on the same graph sheet, indicating clearly all vertices and their
coordinates:
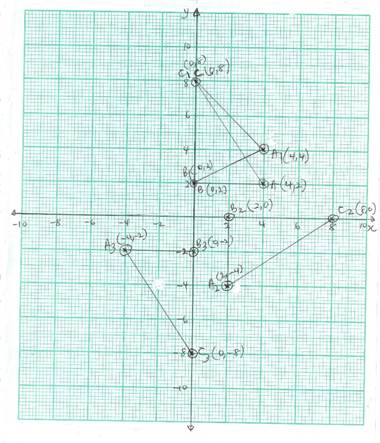
(i). triangle ABC with vertices A(4, 2), B(0, 2) and C(0, 8);
(ii). the image Δ A1B1C1 of Δ ABC under a mapping
→ 
, where A → A1, B → B1 and C →C1;
(iii). the image ΔA2B2C2 of ΔABC under a clockwise rotation of 90o about the origin where A → A2, B → B2 and C → C2;
(iv). the image Δ A3B3C3 of Δ ABC under an enlargement with the scale factor -1 where A → A3, B → B3 and C → C3.
Observation
The Chief Examiner reported that this question was the most unpopular question and majority of those who attempted it performed poorly. They were reported to have answered parts (a), (b)(i) and (b)(ii) only. They did not go further.
In part (a), candidates were expected to use the given scale and draw on a graph sheet the two perpendicular axis (i.e. the x and y axes). Thereafter, they would plot the points A(4, 2), B(0, 2) and C(0, 8),join the points to form the triangle ABC and label the vertices accordingly. The points A1 (4, 4), B1 (0, 2) and C1 (0, 8) were obtained by substituting the values of the x and y coordinates of the points A(4, 2), B(0, 2) and C(0, 8) respectively into the vector 
. They were expected to plot these points on the same graph, and label the coordinates. Candidates were also expected to know that when a point P(x, y) is rotated 90o in the clockwise rotation about the origin, its image would be the point P’(y, -x). This implied that the image of points A(4, 2), B2(0, 2) and C(0, 8) under a clockwise rotation of 90o about the origin were respectively A2(2, -4), B2(2, 0) and C3(8, 0). These points would also be plotted on the same graph. The image A3(-4, -2), B3(0, -2) and C3(0, -8) were obtained by multiplying the points A, B and C respectively by the scale factor, -1. The expected graph was:
