|
Question 10 |
- The total surface area of two spheres are in the ratio 9 : 49. If the radius of the
smaller sphere is 12 cm, find, correct to the nearest cm3,the volume of the bigger sphere.
- A cyclist starts from a point X and rides 3 km due West to a point Y. At Y, he changes direction and rides 5 km North-West to a point Z.
(i) How far is he from the starting point, correct to the nearest km?
(ii) Find the bearing of Z from X, to the nearest degree. |
| _____________________________________________________________________________________________________ |
|
This question was reportedly attempted by majority of the candidates and they performed well in it. In part (a), candidates were able to solve the problem on ratio correctly to obtain the radius of the bigger sphere as follows: If r = radius of smaller sphere = 12 cm and R = radius of bigger sphere, then 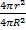 = = 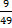 i.e. i.e. 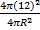 = = 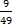 which gave R = 28 cm. Thus the volume of the bigger sphere = which gave R = 28 cm. Thus the volume of the bigger sphere = 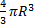 = 91989 cm3. = 91989 cm3.
In part (b), candidates’ performance was not as good as it was in part (a). A few of them did not represent the information on the correct diagram. Others were not able to obtain the required bearing of Z from X. Notwithstanding, candidates showed good knowledge of the topic. Candidates were expected to draw the diagram as shown:
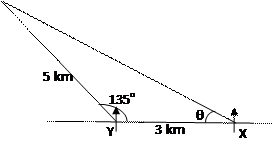
The required distance = |XZ| = 32 + 52 – 2(3)(5)cos 135o = 7 km to the nearest km. Using the sine rule, 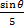 = = 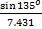 . This implied that sin θ = . This implied that sin θ = 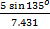 = 0. Hence θ = sin-1() = 28o to the nearest degree. Bearing of Z from X = 270 + 28 = 298o = 0. Hence θ = sin-1() = 28o to the nearest degree. Bearing of Z from X = 270 + 28 = 298o |
|
|
|



