This was also another question where candidates’ performance was reportedly very poor. According to the report, although the question was quite unpopular, more candidates attempted part (a) than part (b) and their performance was better in part (a) than in part (b).
In part (a), candidates were expected to factorize each expression, invert the fraction on the right hand side and cancel out the expressions that are the same

330
i.e. 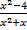  divided by  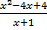  = 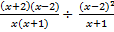  = 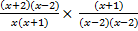 =  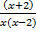.  It was also observed that some candidates could not factorize the expressions correctly.
In part (b), candidates’ performance was reported to be poor. Majority of the candidates displayed weakness in reading from the graph. WAEC was commended for asking this question and encouraged to set such questions regularly so that teachers as well as candidates would be motivated to learn the topic.
The roots of the equation ax2 + bx + c = mx + k was gotten from the graph by reading the            x-coordinate of the point of intersection of the curve and the straight line graphs which were         x = -1.5 and 1.5. The line of symmetry of the curve was x = 0.5. To determine the values of the constants a, b and c, candidates were expected to substitute the coordinates of each of the points L, M and N in the quadratic equation and solve the resulting simultaneous equation thus:

Substituting M(0,2) into the equation we have 2 = a(0)2 +b(0) + c. Therefore, c = 2. Substituting L(-1, 0) into the equation we have 0 = a(-1)2 + b(-1) + 2.  i.e. a – b + 2 = 0 (eqn. 1). Similarly, substituting N(2, 0) into the equation we have 0 = a(2)2 + b(2) + 2.  i.e.  4a + 2b + 2 = 0 (eqn. 2). Solving eqn. 1 and 2 simultaneously gave a = -1 and b = 1. Thus, the quadratic equation was         y = -x2 + x + 2