|
Question 8 |
- Given that sin x = 0.6 and 0o ≤ × ≤ 90o, evaluate 2 cos x + 3 sin x, leaving your answer in the form
 , where m and n are integers.
(b)
In the diagram, a semi-circle WXYZ with centre O is inscribed in an isosceles triangle ABC. If |AC| =|BC|, |OC| = 30 cm and AĈB = 130o, calculate, correct to one decimal place, the
- radius of the circle;
- area of the shaded portion.
(Take π =  )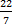
|
| _____________________________________________________________________________________________________ |
|
|
|
|
|
. Hence 2cos x + 3sin x = 2(
+ 3(
) = 
. 
and 
as radii and that lines AC and BC were tangents to the semi-circle at points X and Y respectively. They were also expected to recall that tangents and radii were perpendicular at the point of contact. With this information, candidates were expected to show that |OX| = |OC| sin 65o = 30sin 65o = 27.7 cm. Area of semi-circle = 
(radius)2 = 
(30sin 65o)2 = 1161.7cm2. Since the triangle is isosceles, then ∠AOC = 90o and |OA| = |OB| = 30tan 65o. Therefore |AB| = 2 
30tan 65o = 60 tan 65o. Area of the triangle = ½ base 
height = 
60tan65o
30 = 1930.1 cm2. Hence area of shaded part = 1930.1 – 1161.7 = 768.4 cm2