It was reported that part (a) of this question was poorly attempted by majority of the candidates who attempted it. The Chief Examiner opined that this may be due to the fact that the topic was newly introduced into the curriculum for General Mathematics.
Candidates were expected to complete the table by multiplying the figures, divide the result by 11 and record the remainder to obtain:
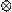
|
1 |
5 |
9 |
10 |
1 |
1 |
5 |
9 |
10 |
5 |
5 |
3 |
1 |
6 |
9 |
9 |
1 |
4 |
2 |
10 |
10 |
6 |
2 |
1 |
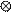
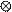
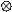
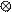
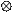
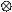 From the table,9 5 = 1 and 10 10 =1. Therefore, (9 5) (10 10) =1 1=1. Similarly, the number that would multiply 10 to have 2 is 9. Therefore, the truth set of
From the table,9 5 = 1 and 10 10 =1. Therefore, (9 5) (10 10) =1 1=1. Similarly, the number that would multiply 10 to have 2 is 9. Therefore, the truth set of
10 x m = 2 was {9}. The number that would multiply itself to have 4 is 9. Therefore the truth set of n x n = 4 was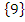 .
.
It was also reported that some of the candidates who were able to solve the question did not express them as sets.
In part (b), the Chief Examiner observed that more work needed to be done by both teachers and candidates in solving word problems. Majority of the candidates were reported not to solve this problem correctly. According to the report, while some of them
could obtain the first equation, majority of them could not obtain the second equation. The few of them who were able to obtain 51 and 68 failed to express the answer as a fraction. Candidates were expected to show that if  was the fraction, then from the first statement,
was the fraction, then from the first statement, =
= 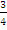 . i.e. 4x = 3y -------- eqn.(1). From the second statement, 2x = y + 34 or y = 2x – 34 --------eqn. (2). Substituting 2x – 34 for y in eqn. (1) gave
. i.e. 4x = 3y -------- eqn.(1). From the second statement, 2x = y + 34 or y = 2x – 34 --------eqn. (2). Substituting 2x – 34 for y in eqn. (1) gave
4x = 3(2x – 34). Solving this equation gave x = 51. Substituting 51 for x in eqn. (2) gave y = 68. Therefore the fraction was 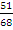 .
.



