Question 10
- If
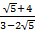 -
- 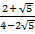 = a + b
= a + b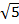 , find the values of a and b.
, find the values of a and b. - (i) Evaluate:
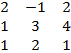 .
.
(ii) Using the result in 10(b)(i), find, correct to two decimal places, the value of x in the system of equations.
2x – y + 2z + 5 = 0
x + 3y + 4z – 1 = 0
x + 2y + z + 2 = 0
Observation
The Chief Examiner reported that this question was attempted by majority of the candidates and they performed very well in it. In part (a), majority of the candidates were reportedly able to apply the method for rationalizing surds with binomial denominators but some of them could not simplify correctly, thereby missing the marks for accuracy. Candidates were expected to find the difference of the surds as follows: ![]() -
- ![]() =
= ![]() -
- ![]()
= ![]() +
+ ![]() =
= ![]() +
+ ![]() . This implied that a =
. This implied that a = ![]() and b = 1.
and b = 1.
In part (b)(i), majority of the candidates calculated the determinants correctly to obtain
Δ =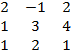 = 2
= 2![]() + 1
+ 1![]() + 2
+ 2![]() = 2(3 – 8) + (1 – 4) + 2(2 – 3) = -15.
= 2(3 – 8) + (1 – 4) + 2(2 – 3) = -15.
In part (b)(ii), candidates were expected to rewrite the system of equations as
2x – y + 2z = -5
x + 3y + 4z = 1
x + 2y + z = -2
which expressed in matrix form gave 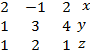 =
= ![]()
Δx = 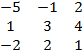 = -5
= -5![]() +
+ ![]() +
+ ![]() = 25 + 9 + 16 = 50.
= 25 + 9 + 16 = 50.
Therefore, x = ![]() =
= ![]() = -3.33.
= -3.33.
