Question 9
- The functions f: x
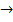 x2 + 1 and g: x
x2 + 1 and g: x 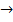 5 – 3x are defined on the set of real numbers, R.
5 – 3x are defined on the set of real numbers, R. - State the domain of f-1, the inverse of f.
- Find g-1(2).
Observation
The Chief Examiner reported that majority of the candidates attempted this question. The report further stated that while majority of the candidates were able to obtain the inverse function, f-1, some of them could not state the domain of f-1. Candidates were expected to show that if f-1 was the inverse of f, then f(f-1(x)) = x. Since f(x) = x2 + 1, then f(f-1(x)) = (f-1(x))2 + 1 = x. This implied that (f-1(x))2 = x – 1.
Hence, f-1(x) = ![]() . f-1(x) will be real if x ≥ 1. Therefore, domain of f-1 =
. f-1(x) will be real if x ≥ 1. Therefore, domain of f-1 =
Df-1 = {x: x ≥ 1}. g(x) = 5 -3x, therefore, g(g-1(x)) = 5 – 3(g-1) = x. This implied that g-1(x) = ![]() . g-1(2) =
. g-1(2) = ![]() = 1. In part (b), majority of the candidates failed to recognize that the numerator and the denominator of the integrand were equal and so would cancel out. Hence, the integral would become
= 1. In part (b), majority of the candidates failed to recognize that the numerator and the denominator of the integrand were equal and so would cancel out. Hence, the integral would become ![]() =
= ![]() = 2. Majority of the candidates applied the substitution method which took them a longer time to get the answer.
= 2. Majority of the candidates applied the substitution method which took them a longer time to get the answer.
