Question 10
(a) Without using Mathematical tables or calculators, simplify:
(a) Without using Mathematical tables or calculators, simplify:
2 tan 60o + cos 30o / sin 60o
(b) From an aeroplane in the air and at a horizontal distance of 1050 m, the
angles of depression of the top and base of a control tower at an instance
are36o and 41o respectively. Calculate, correct to the nearest metre, the:
(i) height of the control tower;
(ii) shortest distance between the aeroplane and the base of the
control tower.
2 tan 60o + cos 30o
sin 60o
(b) From an aeroplane in the air and at a horizontal distance of 1050 m, the
angles of depression of the top and base of a control tower at an instance
are36o and 41o respectively. Calculate, correct to the nearest metre, the:
(i) height of the control tower;
(ii) shortest distance between the aeroplane and the base of the
control tower.
Observation
The Chief Examiner reported that part (a) of this question was well attempted by majority of the candidates. However, it was also reported that a few of them used calculator when the rubrics stated otherwise. A few others were reported not to rationalize the denominator of the resulting surd correctly. Candidates were expected to recall the trigonometric identities and substitute them into the given expression to have ![]() =
= ![]() =
= ![]() =
= ![]() = 5.
= 5.
In part (b), it was reported that candidates’ performance was poor. According to the report, majority of the candidates did not represent the given information in a diagram. Only the few who drew the correct diagram got the question right. Teachers as well as candidates were encouraged to put in more effort at translating word problems to both Mathematical language and diagrams. Candidates were expected to illustrate the given information in a diagram as shown:
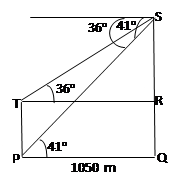
From the diagram, |SR| = 1050tan 36o = 762. 8697 m, |SQ| = 1050tan 41o = 912.7511 m. Therefore, height of control tower = |TP| = |RQ| = 912.7511 – 762.8697 = 150 m, correct to the nearest metre. The shortest distance between the aeroplane and the base of the control tower = |SP| = ![]() = 1391 m, correct to the nearest metre.
= 1391 m, correct to the nearest metre.
