Question 2
(a) Solve the inequality: 4 + ¾ (x + 2) ![]() 3/8x + 1
3/8x + 1
(b)
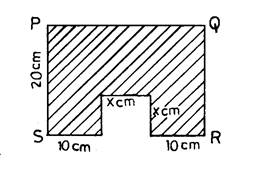
The diagram shows a rectangle PQRS from which a square of side x cm has been cut. If the area of the shaded portion is 484 cm2, find the values of x.
Observation
The Chief Examiner reported that this question was also attempted by majority of the candidates.
In part (a), majority of the candidates were reported to have correctly multiplied through the inequality by the LCM of denominators, which was 8, to obtain 32 + 6(x + 2) ≤ 3x + 8. Simplifying this inequality gave the answer x ≤ -12.
In part (b), a good number of the candidates were reported not to interpret the question correctly and as a result could not obtain the resulting equation. Candidates were expected to show that the area of the shaded portion = area of rectangle – area of the square. Here, length of rectangle = (20 + x) cm and breadth = 20 cm. Therefore, 484 cm2 = (20 + x)(20) – x2. Expanding the bracket and simplifying gave the equation x2 – 20x + 84 = 0. Solving this equation gave the values of x as 6 cm and 14 cm.
