Question 11
(a) Make m the subject of the relation h =![]() .
.
(b)
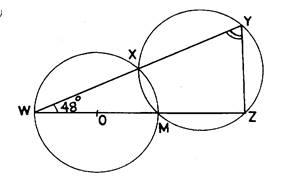
In the diagram, WY and WZ are straight lines;O is the centre of circle
WXM and ÐXWM = 48o. Calculate the value of ÐWYZ.
(c) An operation Å is defined on the set X = {1, 3, 5, 6} by
mÅn = m + n + 2 (mod 7), where m, n ÎX.
` (i) Draw a table for the operation.
(ii) Using the table, find the truth set of:
I. 3 Å n = 3;
II. nÅn = 3.Observation
This question was reported not to be attempted by majority of the candidates. The report further stated that majority of the candidates who attempted the question performed better in part (a) than in parts (b) and (c).
In part (a), majority of the candidates were reported to have cross multiplied correctly to have hdm + hdp = mt. Bringing like terms together and simplifying gave m = ![]() .
.
In part (b), candidates’ performance was reported to be poor. Majority of them did not apply the appropriate circle theorems correctly. They were expected to join XM. Then, ∠WXM = 90o (angle on a semi-circle), ∠WMX = 42o (sum of angles of a triangle is 180o). Therefore, ∠WYZ = 42o (exterior angle of a cyclic quadrilateral).
Part (c) was reported to be attempted by only a few candidates whose performance was described as fair. Many of those who got the table right did not put their final answer in curly brackets. They were asked to find the truth set which implied that the final result was expected to be a set. The expected table was obtained by carrying out the addition in modulo 7 e.g. if m = 5 and n = 5, the mÅm = 5 Å 5 = 5 + 5 + 2 (mod7) = 12(mod 7) = 5
|
1 |
3 |
5 |
6 |
1 |
4 |
6 |
1 |
2 |
3 |
6 |
1 |
3 |
4 |
5 |
1 |
3 |
5 |
6 |
6 |
2 |
4 |
6 |
0 |
Using the table, the set of values of n which satisfied 3Ån = 3 was {5} while the set of values of n which satisfied n Ån = 3 was { } or ![]() .
.
