Question 3
(a) The ratio of the interior angle to the exterior angle of a regular polygon is 5 : 2.
Find the number of sides of the polygon.
(b)
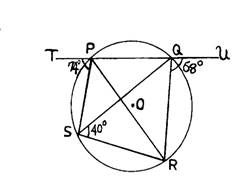
The diagram shows a circle PQRS with centre O, ÐUQR = 68o
ÐTPS = 74o and ÐQSR = 40o. Calculate the value of ÐPRS.
Observation
This question was also reported to be very popular among the candidates but they performed poorly in it. According to the report, their responses indicated a poor knowledge of geometry and teachers were encouraged to emphasize this area of the syllabus.
In part (a), candidates were expected to recall the formula for the sum of the interior angles and exterior angles of a polygon respectively. However, majority of them were reported not to show that each interior angle of a regular polygon was ![]() while each exterior angle was
while each exterior angle was ![]() .Since the ratio was 5 : 2, it implied that
.Since the ratio was 5 : 2, it implied that ![]() =
= ![]() i.e.
i.e. ![]() =
= ![]() =
= ![]() . Simplifying gave n = 7.
. Simplifying gave n = 7.
In part (b), majority of the candidates were reported not to apply the circle theorems correctly.They were expected to show that from the diagram, ∠RSQ = ∠RPQ (angles in the same segment). This implied that ∠PRQ = 68o – 40o = 28o (exterior angle of triangle PQR = sum of the two opposite interior angle). ∠TPS = ∠SRQ = 74o (TPS is the exterior angle of cyclic quadrilateral PQRS). Therefore, the required angle PRS = 74o – 28o = 46o
