Question 13
The table shows the marks scored by some candidates in an examination.
Marks (%) |
0-9 |
10-19 |
20-29 |
30-39 |
40-49 |
50-59 |
60-69 |
70-79 |
80-89 |
90-99 |
Frequency |
7 |
11 |
17 |
20 |
29 |
34 |
30 |
25 |
21 |
6 |
- Construct a cumulative frequency table for the distribution and draw a cumulative frequency curve.
- Use the curve to estimate, correct to one decimal [place, the:
(i) lowest mark for distinction if 5% of the candidates passed with distinction;
(ii) probability of selecting a candidate who scored at most 45%.
Observation
The Chief Examiner reported that this question was attempted by majority of the candidates. According to the report, majority of them were able to construct the cumulative frequency table, a little less were able to determine a suitable scale and drew the cumulative frequency curve correctly but majority of them were unable to read from the curve. Teachers were encouraged to put in more effort at correcting this trend so that their performance may improve in subsequent examinations. Candidates were expected to obtain the following cumulative frequency table:
Class interval |
CLASS BOUNDARIES |
FREQUENCY |
CUMULATIVE FREQUENCY |
|
LOWER |
UPPER |
|||
0 – 9 |
-0.5 |
9.5 |
7 |
7 |
10 – 19 |
9.5 |
19.5 |
11 |
18 |
20 – 29 |
19.5 |
29.5 |
17 |
35 |
30 – 39 |
29.5 |
39.5 |
20 |
55 |
40 – 49 |
39.5 |
49.5 |
29 |
84 |
50 – 59 |
49.5 |
59.5 |
34 |
118 |
60 – 69 |
59.5 |
69.5 |
30 |
148 |
70 - 79 |
69.5 |
79.5 |
25 |
173 |
80 – 89 |
79.5 |
89.5 |
21 |
194 |
90 - 99 |
89.5 |
99.5 |
6 |
200 |
Using the table and an appropriate scale, candidates would draw the cumulative frequency curve as follows:
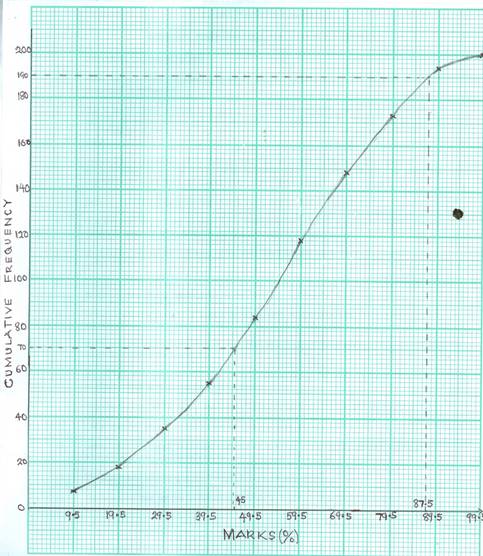
In part (b), candidates were expected to show that if 5% of the candidates passed with distinction, then 95% of them did not pass with distinction. Therefore, candidates would calculate 95% of 200 which was 190. They would then trace 190 from the cumulative frequency axis to the marks axis and read off the point of interception. This was obtained as 87.5% (± 1%). In part (b)(ii), candidates were expected to trace the 45% mark to the cumulative frequency axis and read off the value which was 70. Therefore, the required probability was![]() = 0.35 (± 0.01).
= 0.35 (± 0.01).
- SUMMARY OF EXAMINERS VIEW OF THE STANDARD OF THE PAPER AND CANDIDATES’ PERFORMANCE
|
STANDARD OF THE PAPER |
CANDIDATES’ PERFORMANCE |
HIGHER THAN PREVIOUS YEARS |
5 |
12 |
SAME AS PREVIOUS YEARS |
45 |
12 |
LOWER THAN PREVIOUS YEARS |
1 |
21 |
CANOT BE COMPARED |
- |
- |
NO COMMENTS |
3 |
9 |
- SUGGESTED CRITICAL GRADES
X − 70 - 100
Y − 50 - 59
Z − 40 - 49
